One of the most important features of the Parsing Expression Grammar formalism is that it is packrat parsable. This means that it can be parsed in linear time using a technique called memoization. This technique is also known as tabling in the logic programming community. The basic idea of a Parsing Expression Grammar or PEG is that you have a DSL or a domain specific language which looks exactly like a BNF, except that it is a program and its a parser. Now, these PEGs can be ambiguous and are capable of backtracking. Packrat parsers make the backtracking efficient with caching. How this works, is that the parser remembers the results of all the sub-parsers it has already run, and if it encounters the same sub-parser again, it just returns the result from the previous run. This behaviour makes packrat parsing is a very powerful technique.

When you design a language you typically want to formalize the syntax with a context-free grammar and then you feed it through a compiler and it'll generate a table-driven, bottom-up parser. Then you may have to hack on the grammar until you get it right because in order for the parsers to be efficient they need to be able to look ahead just one symbol so that they know what choice to make as they typically don't support backtracking. Of course there are versions which support infinite backtracking, but that can make your parser very inefficient. So, usually what you try to do in order to get a very efficient parser is you try and turn it into a nice grammar and then you use the generated parser to do what you like.

What exactly we want?
Now, if you read Noam Chomsky, he uses this formalism of BNF to generate languages. What's a language in mathematics? Its a series of strings which satisfy some properties. So, in a context-free grammar like a BNF, we have our left hand side as the non-terminal and our right hand side is a series of terminals and non-terminals. Now, that's context-free! Now, on the other hand, if you had a context-sensitive language, the left hand side would have had some context. But in the case of context-free grammar, the left hand side has no context.
Why do we cling to a generative mechanism for the description of our languages, from which we then labouriously derive recognizers, when almost all we ever do is recognizing text? Why don't we specify our languages directly by a recognizer?
Some people answer these two questions by "We shouldn't" and "We should", respectively.
- Grune & Jacobs, 2008
So, what is it used for? It generates all the strings for the language using that formalism. That's what it's for! But, we have a different problem. We are not Chomsky! We want to write compilers and interpreters for languages. So, we want recognise and reverse engineer the structure. So, actually what we'd like to do is we'd like to use the same formalism for recognizing languages.
Parsing Expression Grammars
The proposal here is to use a rule system to recognize language strings, and instead of taking the description of the grammar and generating a parser, you want the description to be the parser. That's the idea of PEGs — Parsing Expression Grammars — so they model recursive descent parsing.
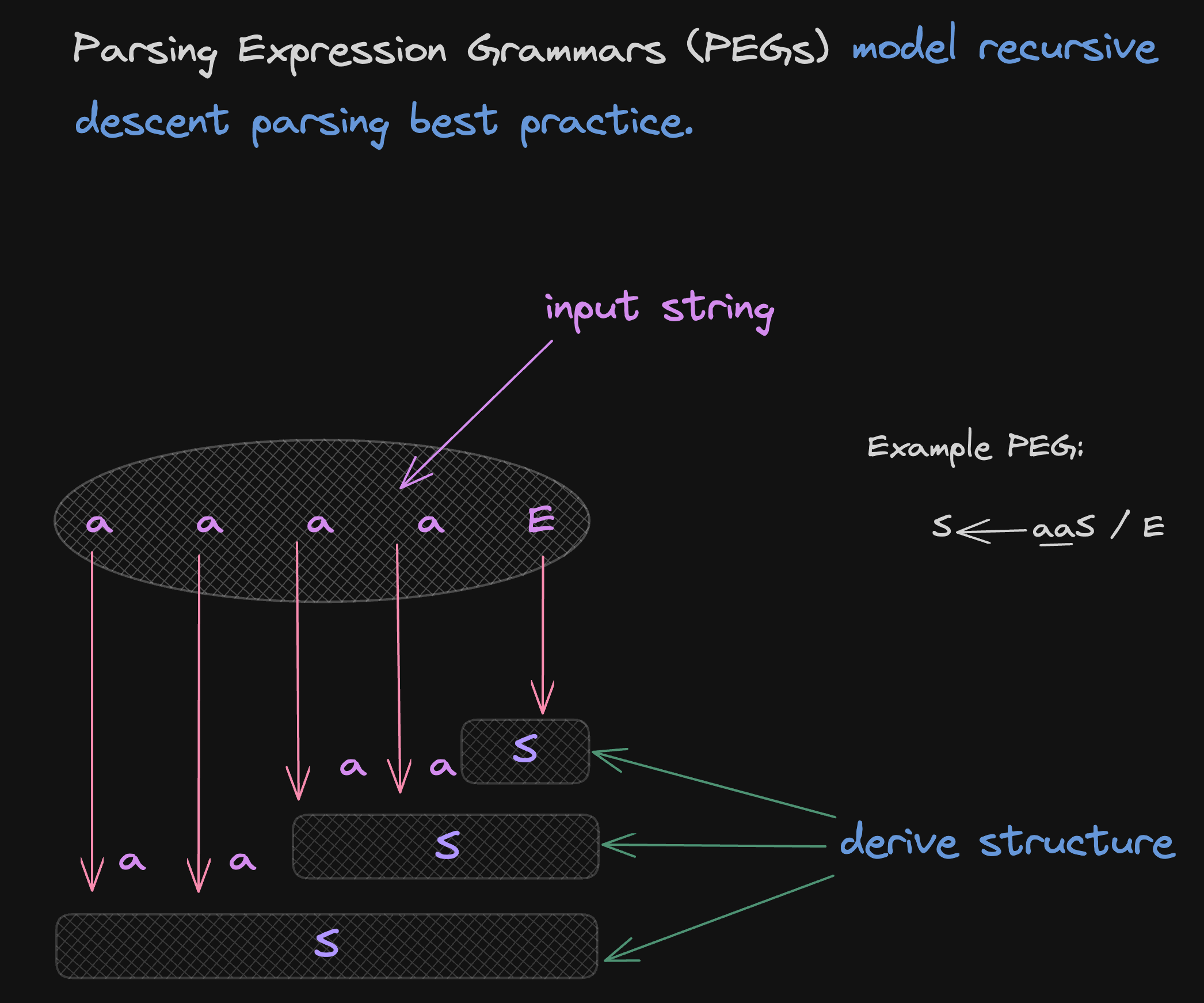
Here are the key benefits of PEGs:
- Simplicity and formalism of CFGs
- Closer match to syntax practices
- More expressive than deterministic CFGs (LL/LR) — here, to be more expressive means you can express things that cannot be captured. For example, context-free grammars cannot express a context-sensitive language, and most languages are ultimately context-sensitive but we handle that in a later phase (in the semantic analysis).
- Natural expressiveness
- Prioritised choice, which actually matches well to a programmatic way of thinking
- Syntactic predicates — using these, we can ask the question, "What's coming next?"
- Unlimited lookahead and backtracking
- Linear time parsing for any PEG! (If you use the packrat parsers, i.e. if you do the caching)
The key assumptions, we make here is that our parsing functions must be
- Stateless — meaning we only depend on the input string
- and we make decisions locally, i.e., return one result or fail
A PEG $P = (\Sigma, N, R, e_s)$
where
- $\Sigma$ is a finite set of terminals (or Character Set)
- $N$ is a finite set of non-terminals
- $R$ is a finite set of rules of the form "$A \leftarrow e$" where $A \in N$ and $e$ is a parsing expression
- $e_s$ is the start expression(a parsing expression)
So, there's not much here. It looks pretty much like BNF with some small differences.
| Table of Symbols and their meanings in PEGs | |
|---|---|
| $\epsilon$ | the empty string |
| $\underline{a}$ | terminal ($a \in \Sigma$), so we can match a string like foo, def, or class. |
| $A$ | non-terminal ($A \in N$) |
| $e_1 e_2$ | sequence — we can have a sequence of things, something like foo, followed by bar. |
| $e_1 / e_2$ | prioritised choice — so, if we have something like foo, followed by foobar, that won't work if we have foobar as the input. That's because, foo will match foo, and the remaining bar will never be matched. So, we better do foobar before foo. |
| $e^?, e^*, e^+$ | optional, zero-or-more, one-or-more |
| &e, !e |
syntactic predicates — they just state something about what's in the input stream but it doesn't consume anything
|
Predictive Parsing
If you have a predictive parser, you use the lookahead to decide which rule you're triggering. And it's fast and it's linear time. But, if you have a backtracking parser, you try alternatives — and if they fail, you backtrack and try another alternative, which can be expensive. So, it's simple and very expressive. It means that you have fewer constraints on designing your specification of your parser and the grammar, it's very convenient, and it makes your job much nicer, but it could take exponential time if you really messed up in the design of the parser.
Take a look at the following code for a
public class SimpleParser {
final String input; // input string
SimpleParser(String input) {
this.input = input;
}
class Result {
int num; // result calculated so far
int pos; // input position parsed so far
Result(int num, int pos) {
this.num = num;
this.pos = pos;
}
}
class Fail extends Exception {
Fail() { super() ; }
Fail(String s) { super(s) ; }
}
...
protected Result add(int pos) throws Fail {
try {
Result lhs = this.mul(pos);
Result op = this.consumeChar('+', lhs.pos);
Result rhs = this.add(op.pos);
return new Result(lhs.num + rhs.num, rhs.pos);
} catch (Fail ex) {
return this.mul(pos);
}
}
...
}
What you see up there is a tiny little language, which just has addition, multiplication and decimal numbers - just zero to nine. That's it! Now, all we gotta do is write our rules. Like this:
- Add $\leftarrow$ Mul $\underline{+}$ Add / Mul
- Mul $\leftarrow$ Prim $\underline{*}$ Mul / Prim
- Prim $\leftarrow$ (Add) / Dec
- Dec $\leftarrow$ $\underline{0}$ / $\underline{1}$ / ... / $\underline{9}$
If you look at the highlighted add rule, I have a multiplication, plus an addition or a multiplication. So, in the parser, I try to match a multiplication, and then I try to consume the "+", and then I try to match the addition, and if I succeed, I return the result. So, my parser is an interpreter — as I calculate and return the result. If anywhere in here we fail, we backtrack and try an alternative rule. Of course, our code up there can fail, but we don't have any alternatives and the whole thing is fucking nested.
At the end, if all goes well, I will have computed a result and what I will have is a hell lot of backtracking. Why? Eh, because multiplication. For example, if I am doing multiplication + addition or multiplication, I have to do the multiplication twice. Similarly, in case of a primitive times multiplication or primitive, I have to do the primitive twice. So, I am doing a lot of work here because these things need to be done over and over again.
Memoized Parsing: Packrat Parsers
Here's a computer science lesson: 50% of the time, or even more, optimizing programs means adding cache. You have to profile the program, find out where it's spending its time (or calculating things twice), and then you say, "oh, let's cache that value!" So memoized parsing in packrat parsers is just that. We just store away the intermediate results of the parsing expressions, and if we encounter the same parsing expression again, we just return the result from the previous run. That's it! That's all we do. So, we just add a cache to our parser and we get a packrat parser.
public class SimplePackrat extends SimpleParser {
HashTable<Integer, Result> [] cache;
final int ADD = 0, MUL = 1, PRIM = 2, HASHES = 3;
SimplePackrat(String input) {
super(input);
this.cache = new HashTable[HASHES];
for (int i = 0; i < HASHES; i++) {
this.cache[i] = new HashTable<Integer, Result>();
}
}
protected Result add(int pos) throws Fail {
if (!this.cache[ADD].containsKey(pos)) {
this.cache[ADD].put(pos, super.add(pos));
}
return this.cache[ADD].get(pos);
}
...
}
Here in the memoized version I have a subclass, and all that happens in the subclass is when I compute something then I store it in in a hash table. This simple technique makes add a few lines of extra code to store the intermediate results, but when we run this, our result is being computed dramatically faster. Pretty slick, right?
Key Takeaways
Now, I don't wanna sell you on Packrat Parsing. Sure, it is definitely useful sometimes. If you are doing backtracking in your recursive descent parser, you might consider using memoization if you have a performance problem. So, yeah! This definitely reduces the the length of time. So, Packrat Parsing:
- has a linear cost — bounded by
size(input)x#(parser rules) - recognizes strictly larger class of languages than deterministic parsing algorithms (LL(k), LR(k))
- is good for scannerless parsing.
Now what does scannerless parsing mean? So what you've seen up until now, if you write a compiler or a parser, you separate lexical analysis from the parsing. So you first recognize lexemes using regular languages, and then you use the full power of context-free grammars to specify the structure. Meaning, you first recognize locally all of these little bits and pieces and then you try and discover the overall structure. Why is that a good thing to do? Because regular expressions are equivalent to state machines — they're fast! But, on the other hand, regular languages are strictly a subset of context-free languages. So, that means you could use BNFs to do the lexical part as well. If you do that, then you have a scannerless parser.
But, why would you want to do that? What's a good use case? For what kind of languages would a scannerless parser be really super useful?
The answer — embedded languages! If one language is embedded inside another, for example, if I have SQL embedded inside Java (or some other query language or DSL) — normally, what I have to do is I have to put it in a string so it's recognized as one lexeme, and then I use another parser to parse that. But if I have a scannerless parser, the scanner part of this parser says, "Okay, now I'm in the Java scope", "Oh, I've entered the SQL scope", "and now I switched to a completely different set of lexemes" — you get the idea! I parse that; and then I say, "Oh, here's the end of the SQL part, I'm back to Java!" — now, let's call it a day! BAM!
You can pop in and out of languages with a scannerless parser, so that's... umm... super interesting.
Finally, let's talk about what Packrat Parsers are not good for:
- General CFG parsing (ambiguous grammars) — because our parser generates at most one output
- Parsing highly "stateful" syntax (e.g., C, C++) — memoization depends on statelessness
- Parsing in minimal space — LL/LR parsers grow in stack depth, not input size
With that, I leave you with a few additional reads:
- Packrat Parsing: Simple, Powerful, Lazy, Linear Time, Bryan Ford
- Packrat Parsing from Scratch, Bruce Hill
- PEG, an Implementation of a Packrat Parsing Expression Grammar in Go, pointlander
- Packrat Parsers Can Support Left Recursion, Alessandro Warth, James R. Douglass, and Todd Millstein
So, what do you think of Packrat Parsers? You know, I added anonymous comments to this site recently — that means you no longer need an account to express your opinions. Go leave an anonymous comment now! (Of course, you get more customization on your profile if you create an account... just saying!)
Alright, see you in the near future! (or maybe like 6 months...)


















Sadly, there are no comments yet. Be the first to leave one!